Introduction to digital certificates
Introduction
Digital certificates are one of the most widely used yet largely misunderstood pieces of technologies in today’s world.They are are largely taken for granted without appreciating the underlying technologies.
This blogpost explains some of the core concepts involved in the usage and implementation of digital certificates and secure systems that rely on them.
Foundation
To begin with, let us look at some of the core concepts involved in building certificates . At first, these might look disconnected. Consider each sub topic here as independent pieces of information and these will converge as we get going.
Hashes / Digest
Here we are talking about cryptographic hash functions and these are not to be confused with hash tables in data structures.
A cryptographic hash function is one which takes an input of arbitrary length and produce a unique digest of fixed length out of it. For example, see the operation of sha256sum hashing algorithm below:
echo "hello world" | sha256sum
a948904f2f0f479b8f8197694b30184b0d2ed1c1cd2a1ec0fb85d299a192a447 -
echo "helloworld" | sha256sum
8cd07f3a5ff98f2a78cfc366c13fb123eb8d29c1ca37c79df190425d5b9e424d -
As you can see, the sha256sum hashing function takes an input string of varying length , and produces a hash/digest of fixed length (256 bytes). Any change in the input string results in a different, unique digest of the same length.
This property of the hashing function can be used to validate the integrity of any arbitrary piece of data. For example, many download sites will display the hash of the file being downloaded along with the hashing algorithm. The hash of the downloaded file can be computed independently and compared to the published hash to ensure that the download was intact.
Another popular use case of this property is to generate unique commit IDs in version controls like Git. The Diff of the changes being committed are passed through the hashing function to generate a unique commit ID of uniform length that represents the changes being committed.
Another important property of hashing function is that it is practically a one way function. Meaning, given a digest, it is impossible to generate the contents that resulted in the digest. The digest in itself does not indicate the length or any other property of the input. Therefore, the same input is needed to regenerate the hash.
These two properties are used to generate a “Message Authentication Code” (MAC) that is used in validating data in secure networks as we will see soon.
Given a digest, the input length and other parameters like input encoding, the input can be computed from a hash. One of the very popular methods used for this is called a
rainbow table. It is a list of precomputed hashes of all alpha numeric combinations of a given length which can be used to reverse map the input that resulted in the string
A hashing function is only one of the methods that can be used to generate a MAC
Encryption and Decryption
Encryption and decryption are conceptually simple operations though they are extremely complex as we get into the implementation details. For a given piece of data $d$ and an encryption key $k$ , we can define two operations $E$ the encryption function and $D$ the decryption function where:
$E(d,k) \rightarrow e$
$D(e,k) \rightarrow d$
Here, $e$ is the encrypted data and $d$ can be obtained from $e$ only if the key $k$ is known.
pardon the inaqurate mathematical notations. style of representation is my only requirement here.
In this case where there is a single key for encryption and decryption, the operation is broadly classified as “symmetric-key cryptography”. Some of the popular examples of symmetric-key algorithms are AES, DES, RC4 etc.
The challenge in this type of cryptography is the secure transmission and storage of the key. In case of network communication, if this is the only type of cryptography available, then the key will have to be transmitted through some medium and this opens up an attack surface where an adversary would be able to get hold of the key.
This is addressed in the case of the next class of cryptographic algorithms called asymmetric key cryptography. In this case, we define a key pair which includes:
- a public key $k_{pu}$
- a private key $k_{pr}$
Here, any data encrypted using $k_{pu}$ can be drypted only using $K_{pr}$. So:
$E(d,k_{pu}) \rightarrow e$
$D(e,k_{pr}) \rightarrow d$
So, your public key can be published so that anyone interested in sending data to you can use it to encrypt it and be assured that it can be decrypted only using your private key that that you have securely stored. Since the private key is never transmitted, it greatly reduces the attack surface.
This approach is generally called a static key based asymmetric cryptography since it involves a stored key and it is not completely secure. When the key pair is generated on the fly and not reused, the pair is called an ephemeral key pair.
Popular algorithms in asymmetric/public-key world are RSA,DSA,ECDSA,DH etc. Of this, only RSA is capable of key exchange as well as practical data encryption. Algorithms like DH are used only for key exchange and DSA algorithms are used for signing digital certificates. We will visit these concepts soon.
In comparison to asymmetric algorithms, symmetric algorithms :
- are faster and more efficient
- are safer for a given key length
- has a fixed over head in terms of increase in the size of encrypted data . (on the contrary RSA for instances increases the size of encrypted data by 10% of input)
key exchange
Key exchange is the process by which two parties can derive a common secret key over an unsecure network while an eavesdropper listening to the exchange process will not be able to derive the same key.
Diffie-Hellman (DH) and RSA are both popular algorithms that can be used for key exchange and the later involves the use of a pre-shared public-key.
One of the popular variants of DH is ephemeral DH (referred to as DHE in the context of TLS) where it does not involve the use of a stored private key for generation and exchange. This ensures “forward secrecy” which means that even if one of the exchanged keys are compromised, it does not lead to compromising other keys generated by the same system.
“Trapdoors” and one way functions
All these cryptographic algorithms revolve around the complexity of reversing some mathematical operation called a one-way function or a trapdoor. An example of such a trap door function is prime factorisation as used in RSA. If two prime numbers are “multiplied” to obtain a composite number, it is computationally exhaustive to generate those exact prime numbers if just the composite is known - provided that the primes are very large. Here multiplication is a modulus based operation and not normal arithmetic multiplication.
Digital Signature
A cryptographic signature or a digital signature is the encrypted MAC of the signed content. For example, when we say that a code file has been digitally signed, it means that a hash of the contents of the file has been generated and the hash has been encrypted with the private key of the signer. This encrypted hash is the signature of the file. The signers public key and the hash are attached to the original file so that a third party can verify the signature by decrypting the signature using the signers public key and comparing it to the hash of the file that he computed independently.
Sometimes, the private key is stored in a special hardware device like a USB dongle and can never be retrieved from it. Any signature operation to be performed will involve the hash being sent to the hardware and the signature being returned by the device.
More on this can be understood once you read about digital certificated below.
keys! keys!! keys!!!
All this while, we have been talking about keys. Essentially,as seen in certificates or key files, they would look like a very large string. However, these are encoded numbers that contains the various parameters that are needed by the algorithm to operate. The encoding is as per the RFC relevant to the algorithm being used.
For example, RSA private key, when decoded can give the following fields:
version Version,
modulus INTEGER, -- n
publicExponent INTEGER, -- e
privateExponent INTEGER, -- d
prime1 INTEGER, -- p
prime2 INTEGER, -- q
exponent1 INTEGER, -- d mod (p-1)
exponent2 INTEGER, -- d mod (q-1)
coefficient INTEGER, -- (inverse of q) mod p
otherPrimeInfos OtherPrimeInfos OPTIONAL
Implementations like OpenSSL has functions that can take the encoded key string and extract these pieces of information from it to operate the corresponding algorithm.
To do this in a terminal, use the following command while passing the key to it.
openssl rsa -text -noout
Digital certificates
A digital certificate is a cryptographically backed proof that can authenticate a resource. Resource can be a domain, a server, a document, a piece of code etc.
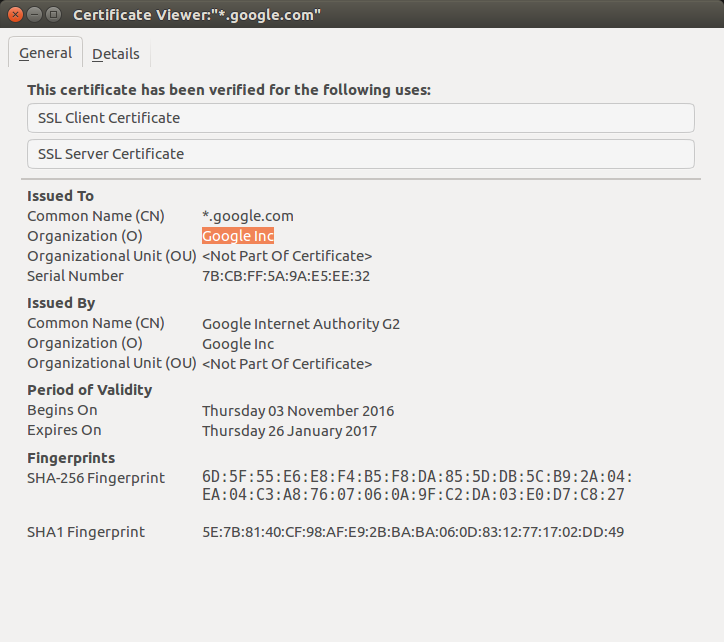
Digital certificates are issued by trusted authorities and will contain the following information:
Serial Number
Subject
Signature Algorithm
Signature
Issuer
Valid-From
Valid-To
Key-Usage
Public Key
Fingerprint Algorithm
Fingerprint
Here, subject is the entity for which the certificate is issued. This information will be verified by the certificate issuing authority (CA).
The most commonly used formate to store these details is the X509 specification. Once these pieces of information is passed through a X509 encoder, the output will be a string that can be safely stored and passed through the network.
A sample certificate stored in the browser looks like this:
As an entity (a server, a company or even a person), the following steps are to be followed to get a digital certificate.
- Generate a public and private key pair and secure the private key.
- Generate a certificate signing request (CSR) and send it to the CA along with proof of identity on the subject information in the request and certificate fee.This request would also contain the public key algorithm and public key from step 1.
- The CA will add the signer details (including the CA public key, CA ID etc), signature and hashing (fingerprint) algorithms, validity dates, usage etc into the CSR and form a TBS (to-be-signed) certificate.
- The CA will compute the hash of TBS, encrypt it using his private key and signature algorithm to form the fingerprint and attach it to the TBS to form a digital certificate.
This digital certificate will now be returned to the requester and he can now use it for the purposes listed in the key-usage field.
Going back to the example of signing a code file, when the digital certificate owner wants to sign a document, he uses his securely stored private key to encrypt the hash of the document and attach it to the document along with the digital certificate itself. When the party who received the document wants to verify the signature, he follows the following steps:
- Ignore the fingerprint of the certificate. Now this is the same as the TBS that the CA used to generate the fingerprint. Compute the hash of this TBS using the finger print algorithm.
- Decrypt the certificate fingerprint using the CAs signing algorithm and public key to get back the hash of the TBS computed by CA.
- Compare the two hashes from 1 and 2. They will match only if the certificate issued by the CA is intact. If any bit in the certificate including keys, identity information etc has changed, the hash would be different.
- Now that the validity of the certificate has been ensured, we can trust the identity of the signer.
- Compute the hash of the document and keep aside the digest.
- Using the public key of the signer in the certificate, that we just validated, decrypt the signature of the document.
- compare the hashes in steps 5 and 6. They will match only if the contents of the document has not been altered after it was signed.
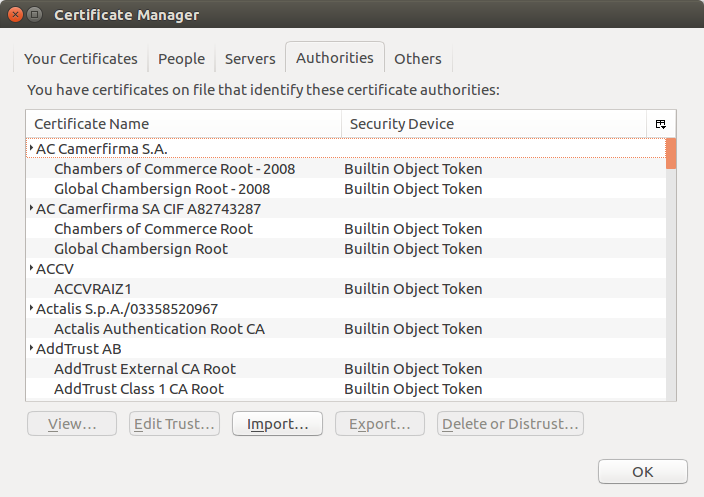
The point to note here is that we have trust the CA blindly and assume that he will not issue certificates to malicious entities or without proper proof of identity. Most operating systems and browsers will have an internal key-store that stores offline copies of root certificates that the CAs that the OS vendor trusts. Public keys from these built in certificates will be used to validate certificates that comes into the system.
Digital certificates and networking
Now that we know the foundational concepts used in digital certificate based authentication and encryption, let us understand how a digital certificate is used in the case of loading a web page and exchanging sensitive data with a server using the example of a browser.
When a browser loads a webpage using the https protocol, it first requests for the digital certificate held by the server. When the server passes on the certificate, it is validated as described in the Digital certificates section of this article. All major browsers will update its internal certificate store of trusted CAs with the latest and greatest root certificates. This list of certificates can be viewed from the browser properties window. These certificates are built into the browser at the time of compilation and will be updated and enhanced on every release.
Here we are effectively offsetting our trust from the CAs to the browser vendor. The impractical alternative is to store certificates of all websites in the internet as a local copy in the browser. This shows the importance of downloading browsers from trusted sources.
Once this validation is complete, the browser will show an indication that the server can be trusted. In case of firefox, it is the green padlock icon in the address bar ( ) .
) .
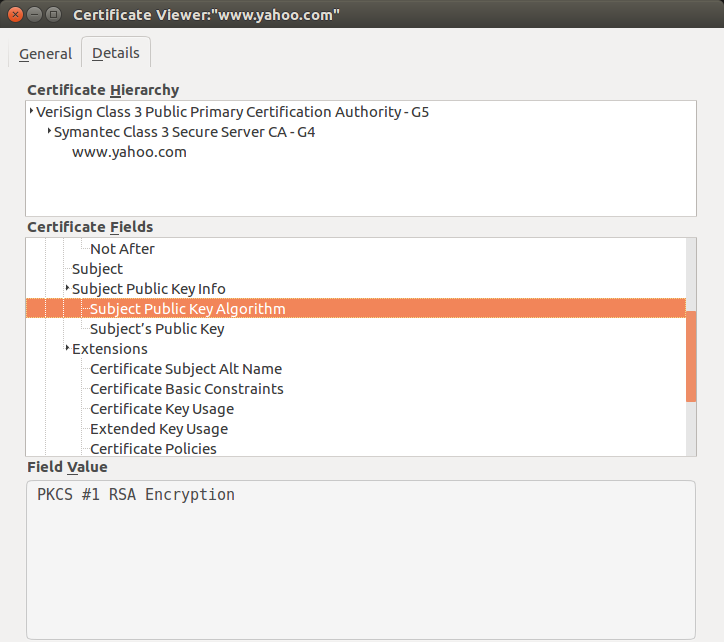
As we discussed before, we need to rely on symmetric cryptographic algorithms for actual encryption of data stream. For this, a secure key needs to be negotiated between the server and the browser. The key exchange algorithm to be used for this will determines using a combination of cypher suite selected for the transaction and the algorithm mentioned in the certificate. For example, in the yahoo certificate shown below, RSA algorithm is to be used.
cypher suite exchange is a process in TLS/SSL handshake where the server and client exchanges the list of cypher suites that they can support and the highest common suite is selected for the session.
In case of mutual authentication, the server application will request a certificate from the client and validate it before giving it access to server resources.






Leave a comment